Hay problemas “superados”, no porque se hayan resuelto, sino por la fatiga de no encontrarles solución. Se aban- donan. Se archivan. Peor aún: se desproblematizan, como dijo Ortega y Gasset. Ya ni se entiende por qué preocupaban.
Así sucede con el famoso problema de las paralelas, sobre el cual Xosé Díaz Díaz ha escrito un libro notable: Dos arquivos xeométricos. Razón e realidade no pensamento de Rafael Dieste. El título juega con otro de Dieste: Dos arquivos do trasno, cuentos breves traducidos por César Antonio Molina para la Colección Austral como De los archivos del trasgo.
Euclides no inventó la geometría. Los astrónomos, agrimensores y constructores de Egipto, Babilonia, India y Grecia tenían conocimientos geométricos. El Teorema de Pitágoras (como después se llamó) era conocido, pero como un saber práctico. La hazaña intelectual de Euclides, lo que nunca se había hecho, fue demostrarlo. Hizo lo mismo para los demás conocimientos, desplegándolos como una serie de teoremas demostrados sucesivamente, unos a partir de otros, con suprema originalidad.
Ya no eran este y aquel conocimiento, sino todo un sistema racional, construido a partir de elementos tan simples como: Desde cualquier punto a cualquier otro se puede trazar una recta (primer postulado). Una recta puede prolongarse indefinidamente (segundo postulado). Sus postulados eran obvios: afirmaciones aceptables sin demostración que, sin embargo, permitían demostrar los conocimientos menos obvios.
La belleza imponente del sistema euclidiano, en comparación con el conjunto disperso de conocimientos anteriores, lo estableció como paradigma del saber. Deslumbró. Todavía dos milenios después, Spinoza adopta ese formato para su Ethica, ordine geometrico demonstrata.
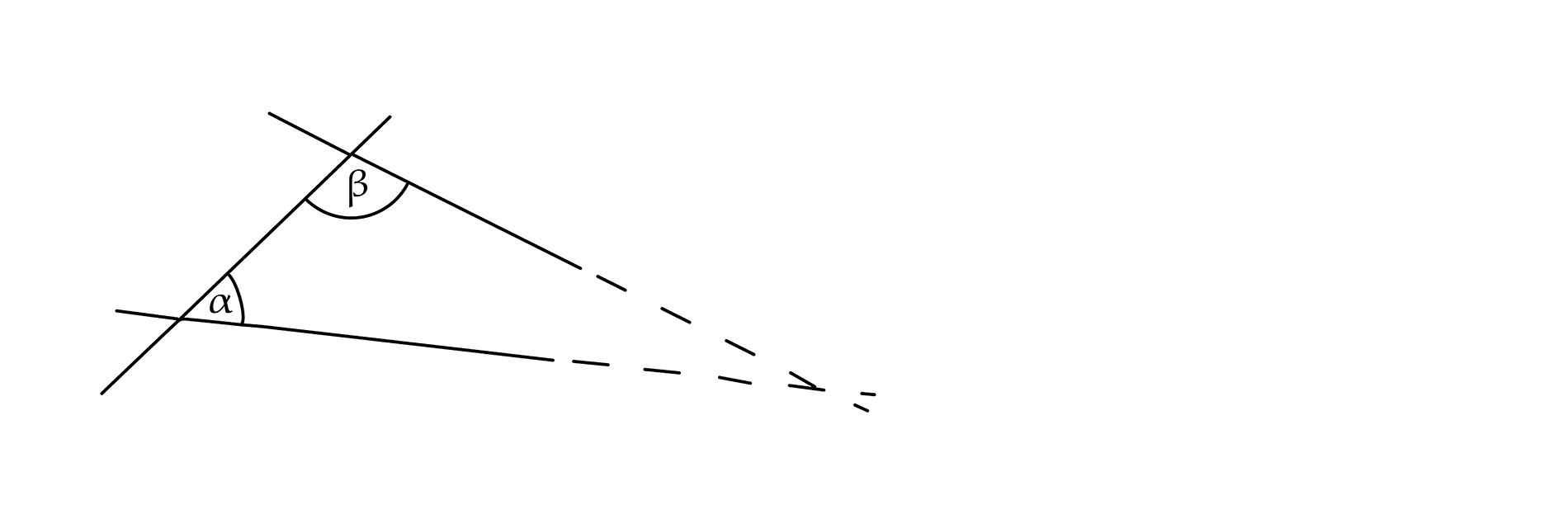
Euclides se topó con un solo conocimiento previo que no encajaba con la misma elegancia: Si una recta cruza otras dos, formando con estas (del mismo lado) ángulos internos cuya suma es menor que dos ángulos rectos [180°], las dos rectas (prolongadas) se cruzan de ese mismo lado (quinto postulado, véase ilustración).
Era verdad, pero no tenía la claridad inmediata de los primeros postulados. Hasta la redacción es complicada. Parece más bien un teorema. Pero Euclides no podía incluirlo en la serie de teoremas porque no pudo demostrarlo. Lo incluyó en la serie de postulados, como diciendo: Ustedes saben que es verdad. Acéptenlo sin demostración.
La propuesta era incómoda y, durante siglos, muchos intentaron lograr lo que Euclides no pudo: demostrar el quinto postulado. Todos fracasaron.
La investigación tuvo un giro sorprendente cuando Giovanni Girolamo Saccheri (1667- 1733) buscó la demostración por reducción al absurdo: Supongamos que las dos rectas prolongadas indefinidamente no se cruzan como dice Euclides, y veamos a qué absurdos se llega. Pero los resultados no fueron contundentes, como esperaba, sino un tanto extraños. Había abierto la puerta a las geometrías no euclidianas.
Por esa puerta entraron Nikolái Lobachevski (1792-1856), Bernhard Riemann (1826-1866) y muchos otros. Desarrollaron lo que Lobachevski llamó una geometría imaginaria, donde se prescindía del quinto postulado y había rectas que se aproximan a distancias cada vez menores y, sin embargo, no llegan a tocarse. Donde había triángulos cuyos ángulos no suman 180°, como demostró Euclides, sino menos o más.
En el siglo XIX se daba por supuesto que la verdadera geometría era la de Euclides, sin perder de vista la presencia inquietante de las otras, nunca refutadas. Sin perder la esperanza de que se refutaran. Hasta hubo intentos de medir físicamente triángulos gigantescos, que sí resultaron de 180°. Pero eso no daba seguridad absoluta, porque toda medición tiene un margen de error.
Todavía en 1903, Mach dijo que la geometría es “la aplicación de matemáticas a las experiencias relativas al espacio”. Es decir, una especie de física, no una baraja de figuras imaginarias, ajenas a la realidad.
Los intentos fallidos por demostrar el quinto postulado desembocaron en una crisis del saber. ¿Cómo que no se puede demostrar si los ángulos de un triángulo suman 180°, menos de 180° o más de 180°? Si esto sucede en las matemáticas, ¿qué certeza tenemos de qué?
En un chiste muy conocido sobre el psicoanálisis, el paciente de un tic acude al psicoanalista y el tic no desaparece. Cuando lo cuestionan por la terapia inútil, la defiende: No fue inútil. Todavía tengo el tic, pero ya no me importa. Superé el problema.
Así se “superó” el problema de las paralelas. Ante el fracaso, se dio por terminada la búsqueda de una solución geométrica y se adoptó una “solución” filosófica: No importa que las geometrías de Euclides, Lobachevski y Riemann sean incompatibles entre sí. Las tres son rigurosas y consistentes. Por lo tanto, las tres son válidas. No se puede demostrar cuál es la buena. Elige la que quieras.
La nueva actitud está implícita en David Hilbert (1862-1943). Construyó una geometría sumamente general que tiene como casos particulares la de Euclides y las otras. Si postulas a llegas a la geometría 1; si postulas b, llegas a la 2; etcétera.
Fue criticado por Frege: “Me parece que usted quiere divorciar completamente la geometría de nuestra intuición del espacio; hacerla una disciplina puramente lógica, como la aritmética.” Pero que el Teorema de Pitágoras sea consistente no basta para afirmar que es verdadero. Hay que demostrarlo. “No puedo admitir la verdad como inferencia de la consistencia.”
Frente al problema que angustió a los matemáticos anteriores, los del siglo XX se liberaron, declarando superada la cuestión. Lo cual desconcertó a muchos creyentes en la ciencia. ¿Así que daba igual una hipótesis que otra, aunque fueran incompatibles? ¿Así que lo científico era renunciar a investigar cuál era la buena?
Fue escandaloso. Ortega y Gasset, al presentar la traducción del libro de Bonola, lo atestigua: “Se oye por dondequiera un monótono treno sobre la cultura fracasada y concluida.”
Husserl, que había estudiado matemáticas, habló sobre La crisis de las ciencias europeas, recogiendo en el título una “frase tan escuchada en nuestros días”. Habló de “quejas generales sobre la crisis de nuestra cultura y del papel atribuido a las ciencias” en esto. La “humanidad europea moderna” había soñado un “edificio único de verdades definitivas y teóricamente trabadas, creciendo hacia el infinito, de generación en generación”.
Se creyó que la ciencia era superior a la filosofía porque los grandes filósofos empiezan desde cero, una y otra vez, y cada uno construye un sistema diferente, en vez de aportar algo a un edificio común, como los científicos. “Si la filosofía fuera una ciencia, después de más de dos mil años de investigación, no existiría hoy en ella semejante falta de teoremas universalmente aceptados” (Brentano, 1874). Pero la coexistencia de geometrías incompatibles rompía la tradición del edificio único. Ponía en crisis los cimientos del saber. Hacía perder la fe en la certidumbre científica.
Parecía que Oswald Spengler tenía razón diagnosticando en 1918 La decadencia de Occidente ante la Gran Guerra (1914-1918). El mundo histórico, político, social, artístico, literario, intelectual y hasta científico parecían desquiciados.
Es muy extraño que Rafael Dieste (1899-1981), un poeta, narrador y dramaturgo celebrado por su obra en gallego y español (véase la Wikipedia en seis idiomas), se haya ocupado de cuestiones geométricas. Se supone que los escritores (y más aún los hispánicos) deben estar exentos de inquietudes científicas. Se supone que la geometría es un volcán apagado, cuyos grandes momentos ya pasaron.
Lo más extraño de todo es que hizo descubrimientos importantes, y que su interés no era ese. Llegó a la geometría preocupado por la cultura, por aquel clima espiritual de crisis que encontró de joven (acentuado en España por la Guerra Civil, 1936-1939).
Hoy está claro que algunas consecuencias de la física del siglo XX (la bomba atómica, por ejemplo) afectan de tal modo la vida humana que toda la humanidad debe hacerse cargo del problema, no solo los especialistas. Bajo esta luz hay que entender el ánimo investigador de Dieste frente a la crisis de la verdad en los cimientos mismos de la ciencia: en la geometría.
Fue profesor de literatura en el Instituto Tecnológico de Monterrey y se entendió muy bien con un grupo de estudiantes de ingeniería que formamos un club de lectura de clásicos de la ciencia. Le pedimos que hablara de los Elementos de Euclides y su charla fue una revelación. Nunca vimos tan claro que las matemáticas se pueden leer, no solo operar, que es lo que suele aprenderse en ingeniería. No solo sabía cien veces más geometría que nosotros, sino que, en forma verdaderamente socrática, nos hizo caer en la cuenta de una problemática inquietante en el “superado” Euclides. Por entonces todavía no encontraba la solución que publicó unos años después en el Nuevo tratado del paralelismo (1956).
Desgraciadamente, en la ciencia se ha vuelto imposible presentar un descubrimiento sin hacer carrera dentro del gremio respectivo: sacar un doctorado, incorporarse a un equipo académico, asistir a convenciones, publicar primero trabajos pequeños firmados con otros y, finalmente, artículos importantes (no libros) en revistas internacionales donde no se publica a los extraños al gremio. Donde nunca se publicarían las investigaciones geométricas que Descartes y Pascal hicieron en su casa.
Afortunadamente, hubo en el gremio coincidencias sobre un teorema fundamental (XXXVI) del Nuevo tratado del paralelismo: “En la hipótesis del paralelismo asintótico [Lobachevski], un par de paralelas es siempre superponible con cualquier otro par de paralelas.”
Me sorprendió encontrar el mismo teorema, demostrado por un procedimiento diferente, cinco años después, en Geometrías no euclidianas del matemático Luis Santaló. Por carta, el profesor Santaló me remitió a Elementare Einführung in die Lobatschewskische Geometrie de Norden, publicado en Berlín Oriental en 1958, aunque originalmente en Moscú en 1953, donde el profesor ruso llegaba al mismo teorema, aunque también por otro procedimiento.
En 1961, el profesor canadiense H. S. M. Coxeter incluyó en Introduction to geometry, por un cuarto procedimiento, un teorema equivalente atribuido a D. W. Crowe (dos triángulos cualesquiera triplemente asintóticos son congruentes). Por carta, Coxeter me aclaró que Crowe no había publicado antes el teorema.
Hay, pues, todos los elementos para documentar como mínimo lo siguiente: entre 1953 y 1961 surgió en la historia de la geometría un nuevo teorema, a través (por lo menos) de cuatro personas y procedimientos diferentes. Y una de estas personas fue Rafael Dieste.
Tratando de entender la crisis de la cultura, llevado por unos problemas que llevan a otros, Dieste había llegado a las fronteras de la ciencia, donde creó a la par que los especialistas.
Sin embargo, a diferencia de los especialistas, que llegaron al teorema y pasaron de largo, Dieste vio que implicaba una inconsistencia monumental con lo que Bertrand Russell (1872-1970) llamó “Axioma de libre movilidad”; desarrollado por Hilbert en el Apéndice iv de sus Fundamentos.
Como si no pudiera creerlo, Dieste dedicó veinte años más a darle toda clase de vueltas a la inconsistencia, a precisarla, a definir con mayor rigor las nociones geométricas implicadas y a simplificar sus demostraciones; trabajos que presenta en ¿Qué es un axioma? (1967) y culminan con las tres demostraciones del quinto postulado de Euclides en su Testamento geométrico (1975).
(Ese título llamó tanto la atención de Roberto Bolaño que hizo del libro y de su autor un tópico novelesco en “La parte de Amalfitano” de 2666.)
Dieste demostró el quinto postulado de Euclides partiendo de axiomas de libre movilidad. Le hubieran gustado a Euclides: “Un punto móvil no pertenece a su trayecto.” Un punto móvil no puede pasar del punto a al punto b sin pasar por un punto intermedio. Con estos axiomas, Dieste reduce al absurdo la hipótesis de Lobachevski.
De igual manera, postulando que “en el espacio existen por lo menos cuatro puntos no situados en un mismo plano” reduce al absurdo la hipótesis de Riemann.
No es fácil descubrir una solución cuando no se ve el problema. Tampoco es fácil reconocerla si aparece donde no era de esperarse. La historia de la ciencia está llena de reconocimientos tardíos, de precursores inesperados. No es imposible que el volcán apagado de la crisis de los fundamentos entre de nuevo en actividad, y que algún especialista descubra lo mismo que Dieste: que la noción de movimiento es decisiva en la cuestión de las paralelas. Tan decisiva que aceptar los axiomas de libre movilidad permite demostrar el quinto postulado de Euclides.
Augurio prometedor. Dieste fue un escritor que amplió sus horizontes a las matemáticas. Xosé Díaz Díaz es un licenciado en matemáticas que amplió sus horizontes a la literatura, y descubrió a Dieste, sobre el cual hizo una tesis de doctorado. Como Lewis Carroll, que escribió un libro sobre Euclides y también Alicia en el país de las maravillas, Díaz Díaz pasó de unas maravillas a otras.
Referencias
Euclides, Elementos de geometría [300 a. C.], tomos I-II (en un solo volumen), bilingüe; precedidos de Los fundamentos de la geometría de David Hilbert; introducción, versión y notas de Juan David García Bacca, México: Universidad Nacional Autónoma de México, Bibliotheca Scriptorum Graecorum et Romanorum Mexicana, segunda edición, 1992, pp. 10-11.
Franz Brentano, Las razones del desaliento en la filosofía [1874] seguido de El porvenir de la filosofía [1893], traducción de Xavier Zubiri, Madrid: Ediciones Encuentro, 2010, p. 9.
Nicolai I. Lobachevski, Pangeometría [1886], traducción de Eli de Gortari, México: Universidad Nacional Autónoma de México, Suplementos del Seminario de Problemas Científicos y Filosóficos, segunda edición, 1987, p. 3.
Bertrand Russell, An essay on the foundations of geometry [1897], New York: Dover, 1956, pp. 149-161.
David Hilbert, Les fondements de la géométrie [1899, el apéndice iv apareció en la segunda edición alemana, 1903], édition critique [y traducción] par Paul Rossier, Paris: Dunod, 1971, pp. 235-241.
Gottlob Frege, On the foundations of geometry and formal theories of arithmetic [1885-1908], compilación, introducción y traducción de Eike-Henner W. Kluge, New Haven and London: Yale University Press, 1971, pp. 14, 20-21.
Ernst Mach, Space and geometry in the light of physiological, psychological and physical inquiry [1906, artículos publicados entre 1901 y 1903], from the German by Thomas J. McCormack, New York: Dover, 2004, p. 124.
Roberto Bonola, Geometrías no euclidianas [1906], traducción de Luis Gutiérrez del Arroyo, nota de José Ortega y Gasset, 2a. ed., Buenos Aires: Espasa Calpe Argentina, 1951, pp. 11-13.
Edmund Husserl, Crisis de las ciencias europeas y la fenomenología trascendental [1936], traducción de Hugo Steinberg, México: Folios Ediciones, 1984, pp. 9, 11, 14.
A. P. [Alexandr Petrovich] Norden, Elementare Einführung in die Lobatschewskische Geometrie [1953], traducción de Waldemar Dege y Klaus-Dieter Rieck, Berlin [Oriental]: veb Deutscher Verlag der Wissenschaften, 1958, p. 67.
Rafael Dieste, Nuevo tratado del paralelismo, Buenos Aires: Atlántida, 1956, pp. 48, 142.
Luis Santaló, Geometrías no euclidianas, Buenos Aires: Eudeba, 1961, p. 39.
H. S. M. [Harold Scott MacDonald] Coxeter, Introduction to geometry, New York: Wiley, 1961, p. 294.
Rafael Dieste, ¿Qué es un axioma? Movilidad y semejanza, Vigo: Ediciones Teseo, 1967.
Rafael Dieste, Testamento geométrico (contiene: Introducción a Euclides, Lobatchevski y Riemann. Los movimientos en geometría. Tres demostraciones del v Postulado), A Coruña: Ediciones del Castro, 1975.
Xosé Díaz Díaz, Dos arquivos xeométricos. Razón e realidade no pensamento de Rafael Dieste, prólogo de Arturo Casas, Rianxo: Axóuxere Editora, 2015. ~
(Monterrey, 1934) es poeta y ensayista.